Домашнее задание №5 к занятию 11.10.2021
Тема: "Кинематические связи"
Попробуйте решить пять задач:
1. Не решая задачу, выберите правильный ответ из четырёх предложенных.
Деревянный кубик со стороной а, плотность которого ρ, плавает в воде. Каким будет изменение глубины погружения кубика Δh, если на воду налить слой масла толщиной l (см. рисунок)? Плотность воды и масла ρв и ρм соответственно.
Возможные ответы:
2. Стержень длиной L касается своими концами вертикальной стенки и горизонтального пола. Он движется, оставаясь всё время в одной и той же вертикальной плоскости, без отрыва от стенки и пола. В некоторый момент времени модуль скорости верхнего конца стержня равен V, а нижнего конца – 2V. Найдите модуль скорости середины стержня в этот момент, а также направление этой скорости относительно горизонтали. На какой высоте от пола находится в этот момент верхний конец стержня?
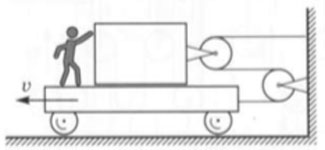
3. Небольшой брусок через систему блоков связан с тележкой нерастяжимой нитью, как показано на рисунке. Тележку приводят в движение с постоянной скоростью 2 см/с. Определите скорость бруска с точки зрения наблюдателя, находящегося на тележке.
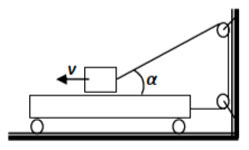
4. Небольшой брусок через систему блоков связан нерастяжимой нитью с длинной тележкой, которая может катиться по горизонтальной поверхности. Брусок кладут на тележку и приводят в движение с постоянной скоростью v = 2 м/с, направленной горизонтально вдоль тележки (см. рисунок). Какую скорость относительно бруска будет иметь тележка в тот момент, когда угол между наклонной нитью и горизонтом составит α = 60°? Считайте, что в указанный момент тележка не доехала до стены, к которой прикреплены блоки.
5. Пластинка в виде равностороннего треугольника ABC движется по плоскости. В некоторый момент скорость точки A направлена параллельно AC, а скорость точки B направлена параллельно BC и равна 15 см/с. Чему равна в этот момент скорость точки C?
Дополнительные задания для желающих
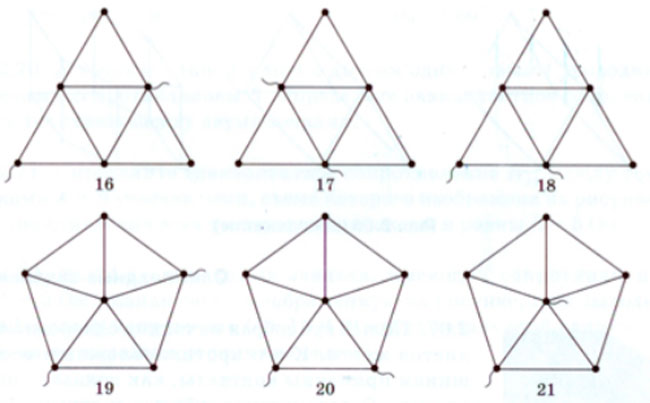
6*. Определите эквивалентные сопротивления проволочных сеток, изображённых на рисунке. Сопротивление каждой ветви любой сетки (вне зависимости от её длины) равно R.
Полезные статьи:
1. Беляев С. Кинематика и связи // Квант. – 1971. №2.
2. Соколов Е. Волшебная формула, или Движение со связями // Квант. – 2012. №1.
3. Соколов Е. Кинематика отрезка // Квант. – 2015. №3.
4. Фистуль М. Кинематика плоскопараллельного движения // Квант. – 1990. №9.