
выпуск 62
ХАРАКТЕР ФИЗИЧЕСКИХ ЗАКОНОВ
 | БИБЛИОТЕЧКА «КВАНТ» выпуск 62 | Pичард Фейнман ХАРАКТЕР ФИЗИЧЕСКИХ ЗАКОНОВ |
ЛЕКЦИЯ 1
Как ни странно, но когда меня (изредка) приглашают играть на бонго, ведущий не считает нужным объявить, что я занимаюсь еще и теоретической физикой. Я объясняю это тем, что искусство мы уважаем больше, чем науку. Художники Возрождения говорили, что интересовать человека должен прежде всего он сам, однако в мире немало других интересных предметов. Ведь и художники любуются закатами, волнами в океане, хороводом звезд на небе... Поэтому иногда не мешает поговорить и о таких вещах. Созерцая их, мы испытываем эстетическое наслаждение. Вместе с тем в явлениях природы есть формы и ритмы, недоступные глазу созерцателя, но открытые глазу аналитика. Эти формы и ритмы мы называем физическими законами. В своих лекциях я хочу погово.рить об особенностях физического закона вообще - поднявшись, если хотите, на одну ступеньку выше самих законов. Передо мной все время будет картина природы, которая возникает после подробнейшего ее анализа, но говорить я буду лишь о самых общих, самых крупных мазках этой картины.
Конечно, подобная тема слишком общая и поневоле располагает к философствованию - начинаешь говорить так расплывчато, что понять тебя может всякий. И тогда считается, что ты решаешь глубокие философские вопросы. Я постараюсь говорить конкретнее, ибо считаю, что мысль простая, но выраженная честно, полезнее туманных намеков. Поэтому в первой лекции, не вдаваясь в общие рассуждения, я просто расскажу об одном физическом законе, дабы вы имели хоть один пример того, о чем впоследствии пойдет отвлеченный разговор. К этому примеру я буду обращаться снова и снова: чтобы проиллюстрировать свою мысль или сделать реальностью то, что иначе могло бы превратиться в абстракцию. В качестве такого примера я выбрал явление гравитации - закон всемирного тяготения. Почему именно его-не знаю. Может быть, потому, что этот великий закон был открыт одним из первых и имеет интересную историю. Вы скажете: "Да, но это старая история, а мне хотелось бы услышать что-нибудь о более современной науке". Может быть, более новой, но не более современной. Современная наука лежит в том же самом русле, что и закон всемирного тяготения. Другими словами, вы просто хотите услышать о более поздних открытиях. Меня же совсем не тяготит перспектива рассказывать вам о законе всемирного тяготения, потому что, описывая его историю, пути и методы его открытия, его основные особенности, я останусь человеком вполне современным.
Этот закон называли "величайшим обобщением, достигнутым человеческим разумом". Но уже из вступительных слов вы, наверное, поняли, что меня интересует не столько человеческий разум, сколько чудеса природы, которая может подчиняться таким изящным и простым законам, как закон всемирного тяготения. Поэтому мы будем говорить не о том, как мы умны, что открыли этот закон, но о том, как мудра природа, которая соблюдает его.
Закон тяготения заключается в том, что два тела действуют друг на друга с силой, которая обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их масс. Математически мы можем выразить этот великий закон формулой
F = G(mm' / r2)
.- некоторая постоянная умножена на произведение двух масс и поделена на квадрат расстояния. Теперь, если я напомню, что под действием силы тело ускоряет свое движение и изменение скорости за секунду обратно пропорционально массе, т. е. скорость меняется тем медленнее, чем больше масса, то я скажу все, что нужно сказать о законе тяготения. Все остальное - математические следствия этих двух фактов. Но я знаю, что нематематику трудно увидеть все такие следствия, и потому постараюсь коротко рассказать вам об истории открытия, о некоторых его следствиях, о том, как оно повлияло на историю науки, о тех тайнах, которые освещает этот закон, об уточнениях, сделанных Эйнштейном, и, возможно, о связи этого закона с другими законами физики.
Вкратце история его такова. Еще древние, наблюдая за движением планет на небе, догадались, что все они, вместе с Землей, "ходят" вокруг Солнца. Позднее, когда люди забыли то, о чем знали прежде, это открытие заново сделал Коперник. И тогда возник новый вопрос: как именно планеты ходят вокруг Солнца, каково их движение? Ходят ли они по кругу и Солнце находится в центре или они движутся по какой-нибудь другой кривой? Как быстро они движутся? И так далее.
Выяснилось это не так скоро. После Коперника снова настали смутные времена и разгорелись зеликие споры о том, ходят ли планеты вместе с Землей вокруг Солнца или Земля находится в центре Вселенной. Тогда человек по имени Тихо Браге (Тихо Браге (1546-1601) - датский астроном) придумал, как можно ответить на этот вопрос. Он решил, что нужно очень внимательно следить за тем, где появляются на небе планеты, точно это записывать и тогда уже выбирать между двумя враждебными теориями. Это и было началом современной науки, ключом к правильному пониманию природы - наблюдать за предметом, записывать все подробности и надеяться, что полученные таким способом сведения послужат основой для того или иного теоретического истолкования. И вот Тихо Браге, человек богатый, владевший островом поблизости от Копенгагена, оборудовал свой остров большими бронзовыми кругами и специальными наблюдательными пунктами и записывал ночь за ночью положения планет. Лишь ценой такого тяжелого труда достается нам любое открытие.
Когда все эти данные были собраны, они попали в руки Кеплера (Иоганн Кеплер (1571-1630) -немецкий астроном и математик, был помощником Браге), который и пытался решить, как движутся планеты вокруг Солнца. Он искал решение методом проб и ошибок. Однажды ему показалось, что он уже получил ответ: он решил, что планеты движутся по кругу, но Солнце лежит не в центре. Потом Кеплер заметил, что одна из планет, кажется Марс, отклоняется от нужного положения на 8 угловых минут, и понял, что полученный им ответ неверен, так как Тихо Браге не мог допустить такую большую ошибку. Полагаясь на точность наблюдений, он решил пересмотреть свою теорию и в конце концов обнаружил три факта.
Сначала он установил, что планеты движутся вокруг Солнца по эллипсам и Солнце находится в одном из фокусов. Эллипс - это кривая, о которой знают все художники, потому что она представляет собой растянутый круг. Дети тоже знают о нем: им рассказывали, что если продеть в кольцо бечевку, закрепить ее концы и вставить в кольцо карандаш, то он опишет эллипс (рис. 1).
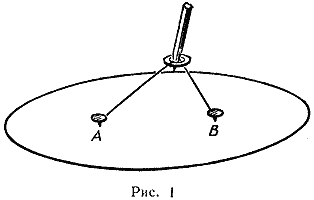
Две точки А и В - фокусы. Орбита планеты - эллипс. Солнце находится в одном из фокусов. Возникает другой вопрос: как движется планета по эллипсу? Идет ли она быстрее, когда находится ближе к Солнцу? Замедляет ли движение, удаляясь от него? Кеплер ответил и на этот вопрос (рис. 2). Он обнаружил, что если взять два положения планеты разделенных друг от друга определенным промежутком времени, скажем тремя неделями, потом взять другую часть орбиты и там - тоже два положения планеты разделенные тремя неделями, и провести линии (ученые называют их радиус-векторами) от Солнца к планете, то площадь заключенная между орбитой планеты и парой линий которые отделены друг от друга тремя неделями всюду одинакова, в любой части орбиты. А чтобы эти площади были одинаковы, планета должна идти быстрее, когда она ближе к Солнцу, и медленнее, когда она далеко от него.
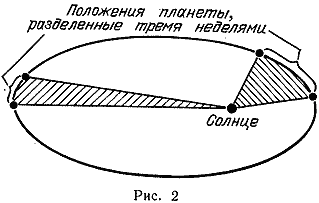
Еще через несколько лет Кеплер сформулировал третье правило, которое касалось, не движения одной планеты вокруг Солнца, а связывало движения различных планет друг с другом. Оно гласило, что время полного оборота планеты вокруг Солнца зависит от величины орбиты и пропорциорционально квадратному корню из куба этой величины. А величиной орбиты считается диаметр, пересекающий самое широкое место эллипса.
Так Кеплер открыл три закона, которые можно свести в один, если сказать, что орбита планеты представляет собой эллипс - за равные промежутки времени радиус-вектор планеты описывает равные площади и время (период) обращения планеты вокруг Солнца пропорционально величине орбиты в степени три вторых, т. е. квадратному корню из куба величины орбиты. Эти три закона Кеплера полностью описывают движение планет вокруг Солнца.
Спросим себя: что заставляет планеты двигаться вокруг Солнца? Во времена Кеплера некоторые люди отвечали, что позади планет сидят ангелы, машут крыльями и толкают планеты по орбитам. Позднее вы увидите, что этот ответ не так уж далек от истины. С той только разницей, что "ангелы" сидят в другом месте и толкают планету к Солнцу.
Тем временем Галилей исследовал законы движения самых обычных предметов, которые были у него под рукой. Изучая эти законы, производя различные опыты, чтобы выяснить, как скатываются шарики по наклонной плоскости, как качаются маятники и т. д. Галилей открыл великий принцип, который называется принципом инерции и состоит вот в чем: если на предмет ничто не действует и он движется с определенной скоростью по прямой линии, то он будет двигаться с той же самой скоростью и по той же самой прямой линии вечно. Как ни странно это звучит для тех, кто пытался заставить шарик вечно катиться по полу, но если бы эта идеализация была верна и на шарик ничто не действовало (например, трение о пол), то шарик все время катился бы с постоянной скоростью.
Затем наступила очередь Ньютона, который раздумывал над таким вопросом: а если шарик не катится по прямой линии, что тогда? И он ответил так: для того чтобы хоть как-нибудь изменить скорость, нужна сила. Например, если вы подталкиваете шарик в том направлении, в каком он катится, то он покатится быстрее. Если вы заметили, что он свернул в сторону, значит, сила действовала сбоку. Силу можно измерить произведением двух величин. Насколько меняется скорость за небольшой промежуток времени? Эта величина называется ускорением. Если ее умножить на коэффициент, называемый массой предмета, то произведение и будет силой.
Силу можно измерить. Например, если мы привяжем к веревке камень и станем крутить его над головой, то почувствуем, что за веревку надо тянуть. Правда, когда камень летает по кругу, величина скорости не изменяется - зато изменяется ее направление. Значит, нужна сила, которая все время тянула бы камень к центру, и сила эта пропорциональна массе. Если мы возьмем два разных предмета и станем раскручивать сначала один, а потом другой с той же самой скоростью, то во втором случае потребуется сила, во столько раз большая, во сколько масса второго предмета больше массы первого.
Таким образом, определив силу, необходимую для того, чтобы изменить скорость тела, мы можем вычислить его массу. Поэтому, решил Ньютон, планете, вращающейся вокруг Солнца, не нужна сила, чтобы двигаться вперед; если бы никакой силы не было, планета летела бы по касательной. Но на самом деле планета летит не по прямой. Она все время оказывается не в том месте, куда попала бы, если бы летела свободно, а ближе к Солнцу (рис. 3). Другими словами, ее скорость, ее движение отклоняются в сторону Солнца. Поэтому ангелы должны так махать крыльями, чтобы все время подталкивать планету к Солнцу.

Но свободное движение не имеет никакой видимой причины. Почему предметы способны вечно лететь по прямой линии, мы не знаем. Происхождение закона инерции до сих пор остается загадкой. В отличие от ангелов свободное движение существует, и, чтобы искривить его, нужна сила. Стало ясно, что источник этой силы. находится где-то около Солнца. И Ньютону удалось доказать, что второй закон Кеплера - закон равенства площадей - прямо вытекает из той простой идеи, что все изменения в скорости направлены к Солнцу. Даже в случае эллиптической орбиты. В следующей лекции я попытаюсь подробно объяснить вам, как это можно сделать.
Этот закон укрепил Ньютона в мысли, что сила, действующая на планеты, направлена к Солнцу и что, зная, как период обращения разных планет зависит от расстояния до Солнца, можно будет определить, как ослабляется сила с расстоянием. Он нашел, что сила обратно пропорциональна квадрату расстояния. До сих пор Ньютон не сказал ничего нового - он лишь повторил другими словами то, что сказал до него Кеплер. Один закон Кеплера равнозначен утверждению, что сила направлена к Солнцу, а другой - утверждению, что сила обратно пропорциональна квадрату расстояния.
Люди рассматривали в телескоп Юпитер со спутниками, обращающимися вокруг него, и им это напоминало маленькую Солнечную систему. Все выглядело так, будто спутники притягиваются к Юпитеру. Луна тоже вращается вокруг Земли и притягивается к ней точно таким же образом. Естественно, возникла мысль, что притяжение действует повсюду. Оставалось лишь обобщить эти наблюдения и сказать, что все тела притягивают друг друга. А значит, Земля должна притягивать Луну так же, как Солнце притягивает планеты. Но известно, что Земля притягивает и обычные предметы: вы, например, прочно сидите на стуле, хотя вам, может быть, и хотелось бы летать по воздуху. Тяготение предметов к Земле было явлением, хорошо известным. Ньютон предположил, что Луну на орбите удерживают те же силы, которые притягивают предметы к Земле.
Насколько падает Луна за секунду, нетрудно сообразить потому, что вы знаете размеры орбиты, знаете, что Луна обходит Землю за месяц и, подсчитав, сколько она проходит за секунду, сможете узнать, насколько круг лунной орбиты отклоняется за секунду от прямой линии, по которой бы летела Луна, если бы Земля ее не притягивала. Эта величина немногим больше 1,25 мм. Луна в 60 раз дальше от центра Земли, чем мы (мы удалены от центра Земли на 6400 км, а Луна - на 378000 км). Значит, если закон обратнопропорциональной зависимости от квадрата расстояния правилен, то предмет у поверхности Земли при падении должен пролетать за секунду 1,25 мм Х 602, потому что на орбите Луны предметы должны притягиваться в 60 Х 60 раз слабее. Итак, 1,25 мм Х 3600 - это примерно 5 м. Измерения Галилея показали, что, падая у поверхности Земли, тела пролетают в секунду 5 м. Это означало, что Ньютон встал на верную дорогу, потому что, если раньше было известно два независимых факта: во-первых, период вращения Луны и величина ее орбиты и, во-вторых, расстояние, которое пролетает падающее тело у поверхности Земли, то теперь эти факты оказались тесно связанными. Эта увлекательная проверка показала, что с теорией Ньютона все обстоит благополучно.
Затем Ньютон сделал еще несколько предсказаний. Ему удалось вычислить, какую форму должна иметь орбита, если закон обратной пропорциональности квадрату расстояния справедлив; он нашел, что орбита должна быть эллипсом, и получил третье подтверждение своего закона. Вдобавок ему удалось объяснить и некоторые другие явления.
Фактически Земля делает то же самое, что и Луна - она движется по кругу. Сила, с которой Луна действует на Землю, уравновешивается - но чем? Как Луна ходит по кругу, чтобы уравновесить притяжение Земли, точно так же ходит по кругу и Земля. Обе они обращаются вокруг общего центра, и силы на Земле уравновешены так, что вода в х притягивается Луной слабее, в у - сильнее и в обоих местах вода вспучивается. Так были объяснены приливы и почему они происходят дважды в сутки.
Прояснилось и многое другое: как Земля стала круглой из-за того, что все ее части притягивали друг друга, как она оказалась не совсем круглой из-за того, что вращается и наружные части ее стремятся прочь сильнее, чем внутренние, почему шарообразны Луна и Солнце и т. д.
С развитием науки измерения производились все точнее и подтверждения ньютоновских законов становились все более убедительными. Первые точные измерения касались спутников Юпитера. Казалось бы, если тщательно наблюдать за их обращением, то можно убедиться, что все происходит согласно Ньютону. Однако выяснилось, что это не так. Спутники Юпитера появлялись в расчетных точках то на 8 мин раньше, то на 8 мин позже, чем полагалось бы согласно законам Ньютона. Обнаружилось, что они опережают график, когда Юпитер сближается с Землей, и отстают, когда Юпитер и Земля расходятся, - очень странное явление.
Рёмер (Олаф Рёмер (1644-1710) - датский астроном), убежденный в правильности закона тяготения, пришел к интересному выводу, что для путешествия от спутников Юпитера до Земли свету требуется определенное время, и, глядя на спутники Юпитера, мы видим их не там, где они находятся сейчас, а там, где они были несколько минут назад - столько минут, сколько требуется свету, чтобы дойти до нас. Когда Юпитер ближе к нам, свет приходит быстрее, а когда Юпитер дальше - свет идет дольше; поэтому Рёмеру пришлось внести поправку в наблюдения на эту разницу во времени, т.е. учесть, что иногда мы делаем эти наблюдения раньше, а иногда позже. Отсюда ему удалось определить скорость света. Так было впервые установлено, что свет распространяется не мгновенно.
История этого открытия показывает, что если какой-то закон верен, то при его помощи можно открыть другой закон. Когда мы убеждены в правильности некоторого закона, но что-то в наших наблюдениях с ним не вяжется, это может указать нам на другое, неизвестное явление. Если бы мы не знали закона тяготения, потребовалось бы гораздо больше времени, чтобы определить скорость света, ибо мы не знали бы, чего ожидать от спутников Юпитера. Этот процесс разросся в целую лавину открытий. Каждое новое открытие давало толчок следующему, и лавина эта движется вот уже 400 лет - в наши дни так же быстро, как и прежде.
Возникла еще одна проблема: планеты не должны двигаться по эллипсам, потому что, согласно законам Ньютона, они не только притягиваются Солнцем, но и притягивают друг друга - слабо, но все же притягивают, и это слегка изменяет нх движение. Уже были известны большие планеты - Юпитер, Сатурн, Уран - и было подсчитано, насколько они должны отклоняться от своих совершенных кеплеровских орбит-эллипсов за счет взаимного притяжения. Когда эти расчеты были закончены и проверены наблюдениями, обнаружилось, что Юпитер и Сатурн движутся в полном согласии с расчетами, а с Ураном творится что-то странное. Казалось бы, еще повод усомниться в законах Ньютона; но главное - не падать духом! Два человека, Адаме и Леверье *), которые выполнили эти расчеты независимо друг от друга и почти одновременно, предположили, что на движение Урана влияет невидимая планета. Они послали письма в обсерватории с предложением: "Направьте ваш телескоп туда-то и вы увидите неизвестную планету". "Что за чепуха,- сказали в одной из обсерваторий,- какому-то мальчишке попала в руки бумага и карандаш, и он указывает нам, где искать новую планету". В другой обсерватории дирекция была легче на подъем - и там открыли Нептун!
Джон Кауч Адаме (1819-1892) - английский математик и астроном; Урбен Леверье (1811-1877)-французский астроном. (Вы можете почитать о них в книге: Саймон Т. Поиски планеты Икс.-М.: Мир, 1966.- Примеч. ред.)
Позже, в начале XX века, выяснилось, что движение планеты Меркурий не совсем правильно. Это вызвало большие волнения и было объяснено только тогда, когда Эйнштейн доказал, что законы Ньютона несовсем точны и надо их несколько изменить.
Возникает вопрос: везде ли действуют эти законы? Выполняются ли они за пределами Солнечной системы? Так вот, рис. 5 показывает, что закон тяготения действует не только в пределах Солнечной системы. Здесь вы видите три фотографии так называемой двойной звезды. На фотографии попала еще одна звезда, и вы можете убедиться, что вращается действительно двойная звезда, а не рамка кадра, хотя сделать это на астрономической фотографии было бы совсем нетрудно. Эти две звезды и в самом деле вращаются, и их орбита изображена на рис. 6.

Рис.5. Три фотографии двойной
звезды, сделанные 21.06.1908,
10.09.1915 и 10.07.1920.Совершенно ясно, что они притягивают друг друга и движутся по эллипсам так, как это и должно происходить. Здесь отмечено последовательное положение звезд в различные моменты времени; звезды движутся по часовой стрелке. Все это кажется прекрасным до тех пор, пока мы не замечаем, что центр орбиты расположен не в фокусе эллипса, а несколько смещен. Значит, что-то неправильно в законе? Нет, просто орбита сфотографирована не анфас, мы смотрим на нее под острым углом. Если вы нарисуете на бумаге эллипс, отметите его фокус и будете смотреть на бумагу под острым углом, то увидите проекцию этого эллипса и фокус проекции не будет совпадать с фокусом самого эллипса. Орбита наклонена в пространстве и именно поэтому выглядит так странно.
А что происходит на больших расстояниях? Эта сила действует между двумя звездами; но будет ли она действовать на расстояниях, которые не в два и не в три, а во много раз превосходят диаметр Солнечной системы? На рис. 7 показан объект, который в 100 000 раз больше, чем Солнечная система; это огромное скопление звезд. Большое белое пятно - не сплошное; оно кажется таким, потому что наши несовершенные инструменты не позволяют разглядеть в нем мелкие детали. На самом же деле оно состоит из очень-очень мелких пятнышек - обычных звезд, и вовсе не слипшихся, а сильно удаленных друг от друга, движущихся взад и вперед в этом большом шаровом скоплении. Это одно из самых прекрасных явлений на небе-такое же прекрасное, как морские волны и закаты. Размещение материала в скоплении совершенно ясно указывает, что звезды в. нем также, связаны взаимным тяготением. Зная примерно расстояние до этой галактики и размещение материала в ней, мы можем приблизительно определить закон сил. действующих между звездами,- приблизительно определить, что и здесь они обратно пропорциональны квадрату расстояния. Точность этих измерений и выкладок, конечно, не может сравниться с точностью, какую мы получаем в Солнечной системе.
 Тяготение действует и на еще больших расстояниях. Наше звездное скопление выглядит незаметной точкой на рис. 8, где показана типичная галактика. И опять-таки ясно, что эта галактика держится как единое целое благодаря какой-то силе. А никакой другой силы, кроме тяготения, здесь предположить нельзя. Когда мы переходим к таким масштабам, мы уже не можем проверить справедливость ньютоновского закона. Но несомненно, что в таких гигантских звездных образованиях - в этих галактиках, которые простираются на 50-100 тысяч световых лет, тогда как расстояние от Солнца до Земли составляет только 8 световых минут, - даже на таких огромных расстояниях действуют силы тяготения.Рис. 7. Шаровое скопление M15 (NGC 7078) в созвездии Пегаса. Это скопление необычно тем, что в своей северо-восточной части содержит маленькую планетарную туманность (K 648). Скопление M15 - сильный источник рентгеновского излучения. Оно удалено на 34 тысячи световых лет (10.5 кпс) и имеет диаметр в 130 световых лет. Фотография сделана 4-метровым телескопом Мэйэлла Национальной обсерватории в Китт-Пик.
Тяготение действует и на еще больших расстояниях. Наше звездное скопление выглядит незаметной точкой на рис. 8, где показана типичная галактика. И опять-таки ясно, что эта галактика держится как единое целое благодаря какой-то силе. А никакой другой силы, кроме тяготения, здесь предположить нельзя. Когда мы переходим к таким масштабам, мы уже не можем проверить справедливость ньютоновского закона. Но несомненно, что в таких гигантских звездных образованиях - в этих галактиках, которые простираются на 50-100 тысяч световых лет, тогда как расстояние от Солнца до Земли составляет только 8 световых минут, - даже на таких огромных расстояниях действуют силы тяготения.Рис. 7. Шаровое скопление M15 (NGC 7078) в созвездии Пегаса. Это скопление необычно тем, что в своей северо-восточной части содержит маленькую планетарную туманность (K 648). Скопление M15 - сильный источник рентгеновского излучения. Оно удалено на 34 тысячи световых лет (10.5 кпс) и имеет диаметр в 130 световых лет. Фотография сделана 4-метровым телескопом Мэйэлла Национальной обсерватории в Китт-Пик.
 Рис. 9 свидетельствует о том, что силы тяготения простираются еще дальше. Это так называемое скопление галактик. Все они собраны в один ком, как и звезды, только этот ком составлен не из звезд, а из "крошек" вроде той, которую вы видите на рис. 8.Рис. 8. Спиральная галактика типа Sc в созвездии Большой Медведицы M101 (NGC 5457) удалена от нас на расстояние 15 млн. световых лет. Гигантское звездное колесо, напоминающее формой и размером Млечный Путь, открывается нашему взгляду почти сверху, причем темные волокна в рукавах - прослойки пыли. Фотография получена с помощью 4-метрового телескопа Мэйэлла Национальной обсерватории в Китт-Пик.
Рис. 9 свидетельствует о том, что силы тяготения простираются еще дальше. Это так называемое скопление галактик. Все они собраны в один ком, как и звезды, только этот ком составлен не из звезд, а из "крошек" вроде той, которую вы видите на рис. 8.Рис. 8. Спиральная галактика типа Sc в созвездии Большой Медведицы M101 (NGC 5457) удалена от нас на расстояние 15 млн. световых лет. Гигантское звездное колесо, напоминающее формой и размером Млечный Путь, открывается нашему взгляду почти сверху, причем темные волокна в рукавах - прослойки пыли. Фотография получена с помощью 4-метрового телескопа Мэйэлла Национальной обсерватории в Китт-Пик.
 Это чуть ли не одна сотая, а может быть, и десятая часть известной нам Вселенной, где мы имеем прямые свидетель ства существования сил тяготения. Таким образом, притя жение Земли не имеет границ, хотя в газетах и пишут по рой, что такое-то тело освободилось от оков земного притяжения. Притяжение становится все слабее и слабее - оно обратно пропорционально квадрату удаления от Земли: каждый раз, когда расстояние до Земли увеличивается вдвое, сила тяготения падает вчетверо и в конце концов теряется в переплетении более сильных полей тяготения других звезд. Вместе с соседними звездами Земля притягивает другие звезды, и они образуют Галактику. Галактика притягивает другие галактики и вместе они образуют скопление - систему галактик. Таким образом, притяжение Земли нигде не кончается, но убывает медленно и строго закономерно, может быть. до самых пределов Вселенной.Рис. 9. На этой фотографии, полученной с помощью 4-метрового телескопа Национальной обсерватории в Китт-Пик, показано гигантское скопление галактик (Абель 2218) на расстоянии 2 млрд. световых лет (красное смещение 0,2), которое выглядит желтоватым. Сильное гравитационное поле этого скопления является причиной искажения изображений более удаленных (голубоватых) скоплений и превращения их в систему концентрических дуг. Уровень искажения позволяет сделать вывод, что скопление Абель 2218 имеет по крайней мере в десять раз большую массу, чем можно приписать видимым галактикам.
Это чуть ли не одна сотая, а может быть, и десятая часть известной нам Вселенной, где мы имеем прямые свидетель ства существования сил тяготения. Таким образом, притя жение Земли не имеет границ, хотя в газетах и пишут по рой, что такое-то тело освободилось от оков земного притяжения. Притяжение становится все слабее и слабее - оно обратно пропорционально квадрату удаления от Земли: каждый раз, когда расстояние до Земли увеличивается вдвое, сила тяготения падает вчетверо и в конце концов теряется в переплетении более сильных полей тяготения других звезд. Вместе с соседними звездами Земля притягивает другие звезды, и они образуют Галактику. Галактика притягивает другие галактики и вместе они образуют скопление - систему галактик. Таким образом, притяжение Земли нигде не кончается, но убывает медленно и строго закономерно, может быть. до самых пределов Вселенной.Рис. 9. На этой фотографии, полученной с помощью 4-метрового телескопа Национальной обсерватории в Китт-Пик, показано гигантское скопление галактик (Абель 2218) на расстоянии 2 млрд. световых лет (красное смещение 0,2), которое выглядит желтоватым. Сильное гравитационное поле этого скопления является причиной искажения изображений более удаленных (голубоватых) скоплений и превращения их в систему концентрических дуг. Уровень искажения позволяет сделать вывод, что скопление Абель 2218 имеет по крайней мере в десять раз большую массу, чем можно приписать видимым галактикам.Закон тяготения отличается от многих других законов. Ясно, что он играет большую роль в механике Вселен ной. И покуда речь идет о Вселенной, этот закон всюду находит практическое применение. Но на Земле, как ни странно, закон тяготения дает нам гораздо меньше практически полезных сведений, чем другие законы физики. Только в этом смысле не типичен выбранный мной пример.
Кстати говоря, невозможно выбрать такой пример, который был бы типичен во всех отношениях. Это удивительное свойство нашего мира.
Единственные практические приложения этого закона, которые мне приходят на ум, это пожалуй, некоторые методы геологической разведки, предсказание приливов и в последнее время расчет движения искусственных спутников и межпланетных станций. Да, и еще одно современное приложение: закон Ньютона позволяет заблаговременно вычислять положения планет астрологам, которые публикуют свои гороскопы в журналах. Поистине мы живем в удивительном мире: все новейшие достижения человеческой мысли используются только для того, чтобы разнообразить чепуху, существующую вот уже две тысячи лет.
Рис. 10. Газовые туманности
в созвездии ЛебедяЗвезды рождаются из газа, который чересчур сжался под действием притяжения. Иногда звезды взрываются, выбрасывают пыль и газы, потом пыль и газы снова собираются и снова образуют звезды - все это похоже на вечное движение.
Как я уже сказал, тяготение действует на огромных расстояниях. Но Ньютон утверждал, что взаимно притягиваются все предметы. А правда ли, что любые два предмета притягивают друг друга? Можем ли мы сами поставить такой опыт, а не гадать, глядя на небо, притягиваются ли планеты?
Вы скажете: "Взвешивание Земли представляет собой почти такую же задачу. Мы знаем силу притяжения, знаем массу объекта, который притягивается, и знаем, насколько он удален, но мы не знаем ни массы Земли, ни постоянной тяготения, а только их произведение". Измерив постоянную и зная, как Земля притягивает предметы, мы сможем вычислить ее массу.
Этот опыт впервые позволил косвенно определить, насколько тяжел, массивен шар, на котором мы живем. Результат его невольно вызывает удивление, и я думаю, что именно поэтому Кавендиш назвал свой опыт "взвешиванием Земли", а не "определением постоянной уравнения тяготения". Между прочим, он одновременно взвешивал и Солнце и все остальное, потому что притяжение Солнца определяется точно таким же способом.
Интересно было проверить закон тяготения еще с одной стороны: пропорционально ли притяжение массе. Мы знаем, что ускорение прямо пропорционально действующей силе и обратно пропорционально массе. Поэтому если сила притяжения в точности пропорциональна массе, то два тела с разной массой должны одинаково менять свою скорость в поле тяготения. Иначе говоря, два различных предмета в вакууме, независимо от их массы, за одинаковое время пролетят по направлению к Земле одинаковые расстояния. Такие опыты ставил еще Галилей на падающей башне в Пизе.
Это означает, например, что какая-нибудь вещь внутри искусственного спутника Земли будет двигаться точно по такой же орбите, как сам спутник, т. е. будет парить внутри него. И все это - следствие того факта, что сила пропорциональна массе, а ускорение обратно пропорционально массе.
Насколько точно это утверждение? На опыте его проверил Этвеш в 1909 г. (Роланд Этвеш (1848-1919) - венгерский физик), а впоследствии более тщательно - Дикке (Роберт Генри Дикке - современный американский физик). Теперь мы знаем с точностью до одной десятимиллиардной, что сила пропорциональна массе. Как удалось добиться такой точности?
Предположим, вы хотите определить, в какой мере подчиняется этому правилу притяжение Солнца. Вы знаете, что Солнце притягивает всех нас. Оно притягивает Землю, но, предположим, вы хотите знать, в точности ли это притяжение пропорционально массе. Сначала опыт был проделан над сандаловым деревом, потом экспериментировали с медью и свинцом, а теперь пробуют на полиэтилене. Земля вращается вокруг Солнца, поэтому инерция отбрасывает земные тела от Солнца тем сильнее, чем больше инерция. Но, согласно закону тяготения, тела притягиваются к Солнцу - и тем сильнее, чем больше их масса. Поэтому если они притягиваются к Солнцу не в той же пропорции, в какой отбрасываются инерцией, то один предмет будет, например, стремиться к Солнцу, а другой - прочь от него. И тогда, прикрепив эти два предмета к коромыслу Кавендиша, мы увидим, что оно повернется по направлению к Солнцу и перекрутит кварцевую нить. На самом деле, однако, нить не перекручивается, и, с той точностью, которую дает этот опыт, мы знаем, что притяжение двух предметов строго пропорционально центробежному эффекту, который обусловлен инерцией. Таким образом, сила притяжения объекта пропорциональна коэффициенту инерции, или, другими словами, массе.
И вот что еще интересно. Обратно-пропорциональная зависимость от квадрата расстояния встречается и в других законах, например в законах электричества. Электрические силы также обратно пропорциональны квадрату расстояния, но уже между зарядами, и невольно возникает мысль, что в этой закономерности таится глубокий смысл. До сих пор никому не удалось представить тяготение и электричество как два разных проявления одной и той же сущности. Сегодня наши физические теории, законы физики - множество разрозненных частей и обрывков, плохо сочетающихся друг с другом. Физика еще не превратилась в единую конструкцию, где каждая часть - на своем месте. Пока что мы имеем множество деталей, которые трудно подогнать друг к другу. Вот почему в этих лекциях я вынужден говорить не о том, что такое закон физики, а о том, что роднит различные законы; мы плохо понимаем их связь. Но интересно, что у них все же есть некоторые общие черты. Обратимся к законам электричества.
Сила и тут изменяется обратно пропорционально квадрату расстояния, но разница в величине электрических сил и сил тяготения поразительна. Пытаясь установить общую природу тяготения и электричества, мы обнаруживаем такое превосходство электрических сил над силами тяготения, что трудно поверить, будто у тех и у других один и тот же источник. Как можно говорить, что одно действует сильнее другого? Ведь все зависит от того, какова масса и каков заряд. Рассуждая о том, насколько сильно действует тяготение, вы не вправе говорить: "Возьмем массу такой-то величины", потому что вы выбираете ее сами. Но если мы возьмем то, что предлагает нам сама Природа (ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами, с нашими мерами), тогда мы сможем сравнивать. Мы возьмем элементарную заряженную частицу, такую, например, как электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.
Вопрос: каково отношение силы тяготения к электрической силе? Тяготение относится к электрическому отталкиванию, как единица к числу с 42 нулями. Это вызывает глубочайшее недоумение. Откуда могло взяться такое огромное число? Если бы у нас когда-нибудь появилась общая теория для двух этих явлений, то как она давала бы такую диспропорцию для двух электронов:
электрическое отталкивание / сила тяготения = 4,17x1042
Каким должно быть общее уравнение, если, решая его для двух видов сил - гравитационного притяжения и электрического отталкивания, мы приходим к такому фантастическому отношению?
Люди ищут этот огромный коэффициент в других явлениях природы. Они перебирают всякие большие числа, а если вам нужно большое число, почему не взять, скажем, отношение диаметра Вселенной к диаметру протона - как ни удивительно, это тоже число с 42 нулями. И вот говорят: может быть, этот коэффициент и равен отношению диаметра протона к диаметру Вселенной? Это интересная мысль, но, поскольку Вселенная постепенно расширяется, должна меняться и постоянная тяготения. Хотя эта гипотеза еще не опровергнута, у нас нет никаких свидетельств в ее пользу. Наоборот, некоторые данные говорят о том, что постоянная тяготения не менялась таким образом. Это громадное число по сей день остается загадкой.
Чтобы покончить с теорией тяготения, я должен упомянуть еще о двух фактах.
Первое. Эйнштейну пришлось видоизменить законы тяготения в соответствии с принципами относительности. Первый из этих принципов гласит, что расстояние х нельзя преодолеть мгновенно, тогда как по теории Ньютона силы действуют мгновенно. Эйнштейну пришлось изменить законы Ньютона. Эти изменения, уточнения очень малы, Одно из них состоит вот в чем: поскольку свет имеет энергию, энергия эквивалентна массе, а все массы притягиваются, - свет тоже притягивается и, значит, проходя мимо Солнца, должен отклоняться. Так оно и происходит на самом деле. Сила тяготения тоже слегка изменена в теории Эйнштейна. Но этого очень незначительного изменения в законе тяготения как раз достаточно, чтобы объяснить некоторые кажущиеся неправильности в движении Меркурия.
Второе. Физические явления в микромире подчиняются иным законам, нежели явления в мире больших масштабов. Встает вопрос: как проявляется тяготение в мире малых масштабов? На него ответит квантовая теория гравитации. Но квантовой теории гравитации еще нет. Люди пока не очень преуспели в создании теории тяготения, полностью согласованной с квантовомеханическими принципами и с принципом неопределенности.
Вы скажете: "Вы все время говорили только о том, что происходит, но не объяснили, что такое тяготение. Откуда оно? Что оно собой представляет? Ведь не хотите же вы сказать, что планета смотрит на Солнце, видит, насколько оно удалено, подсчитывает обратный квадрат расстояния в соответствии с этим законом?" Иными словами, я просто изложил математический закон, но не объяснил его механизма. Возможности этого мы обсудим в следующей лекции "Связь математики с физикой".
Заканчивая лекцию, я хочу отметить некоторые особенности закона тяготения, характерные и для других законов, о которых мы упоминали по ходу разговора.
1. Закон тяготения выражается математически, так же как и другие законы.2. Он не точен; Эйнштейну пришлось видоизменить его, но мы знаем, что он и сейчас не совсем точен, ибо мы еще не связали его с квантовой теорией. Тоже относится и к другим нашим законам - они не точны. Где-то на краю их всегда лежит тайна, всегда есть, над чем поломать голову. Может быть, это - свойство природы, а может быть, и нет, но это свойственно тем законам, которые известны нам сегодня. Может быть, все дело тут в неполноте нашего знания.
3. Но поразительнее всего то, что закон тяготения прост. Его легко сформулировать так, чтобы не оставалось никаких лазеек для двусмысленности и для иного толкования. Он прост и поэтому прекрасен. Он прост по форме. Я не говорю, что он действует просто - движение разных планет, их взаимное влияние могут быть очень запутанными, и определить, как движется каждая звезда в шаровом скоплении, не в наших силах. Закон действует сложно, но его коренная идея проста. Это и роднит все наши законы. Сами по себе они всегда оказываются простыми, хотя в природе действуют сложным образом.
4. И, наконец, закон тяготения универсален. Он простирается на огромные расстояния, и Ньютон, которого интересовала Солнечная система, вполне мог бы предсказать, что получится из опыта Кавендиша, ибо весы Кавендиша, два притягивающихся шара, это маленькая модель Солнечной системы. Если увеличить ее в десять миллионов миллионов раз, то мы получим Солнечную систему. Увеличим еще в десять миллионов миллионов раз - и вот вам галактики, которые притягиваются друг к другу по тому же самому закону. Вышивая свой узор, Природа пользуется лишь самыми длинными нитями, и всякий, даже самый маленький образчик его может открыть нам глаза на строение целого.

Лекция 2. Связь математики с физикой
Первое издание:
Richard Feynman, The character of physical law, A series of lectures recorded by the ВВС at Cornell University USA,
Cox and Wyman LTD London, 1965